【理論】平成28年 問10|スイッチ操作後のRC回路における過渡現象の論説問題
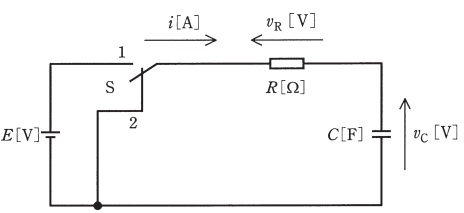
図のように,電圧 \( E \) [V] の直流電源,スイッチ \( \mathrm{S} \),\( R \) [\( \Omega \)] の抵抗および静電容量 \( C \) [F] のコンデンサからなる回路がある。
この回路において,スイッチ \( \mathrm{S} \) を \( 1 \) 側に接続してコンデンサを十分に充電した後,時刻 \( t = 0 \) [s] でスイッチ \( \mathrm{S} \) を \( 1 \) 側から \( 2 \) 側に切り換えた。
\( 2 \) 側に切り換えた以降の記述として,誤っているものを次の (1)~(5) のうちから一つ選べ。
ただし,自然対数の底は \( 2.718 \) とする。
 <
<(1) 回路の時定数は,\( C \) の値 [F] に比例する。
(2) コンデンサの端子電圧 \( v_{\mathrm{C}} \) [V] は,\( R \) の値 [\( \Omega \)] が大きいほど緩やかに減少する。
(3) 時刻 \( t = 0 \) [s] から回路の時定数だけ時間が経過すると,コンデンサの端子電圧 \( v_{\mathrm{C}} \) [V] は直流電源の電圧 \( E \) [V] の \( 0.368 \) 倍に減少する。
(4) 抵抗の端子電圧 \( v_{\mathrm{R}} \) [V] の極性は,切り換え前(コンデンサ充電中)と逆になる。
(5) 時刻 \( t = 0 \) [s] における回路の電流 \( i \) [A] は,\( C \) の値 [F] に関係する。
合格への方程式
過渡現象の基本原理
過渡現象とは、電気回路において状態が変化した直後から定常状態に至るまでの間に生じる一時的な現象のことです。スイッチの開閉、電源の投入・遮断などにより回路の状態が変化すると、リアクトル(インダクタ)やコンデンサを含む回路では過渡現象が発生します。
過渡現象の特徴
1. リアクトルとコンデンサのエネルギー蓄積特性により発生
2. 初期状態から定常状態に至るまでの一時的な現象
3. 時間経過とともに指数関数的に変化
4. 時定数によって収束速度が決まる
過渡現象を理解するためには、リアクトルとコンデンサの基本的な特性を知ることが重要です。
リアクトル(インダクタ)の基本特性
リアクトルに関する基本式:
\[ v_L = L \frac{di_L}{dt} \]
ここで:
\(v_L\; [\mathrm{V}]\):リアクトルの端子間電圧
\(L\; [\mathrm{H}]\):インダクタンス
\(\frac{di_L}{dt}\; [\mathrm{A/s}]\):電流の時間変化率
この式から、リアクトルは電流の変化を妨げる性質を持つことがわかります。
コンデンサの基本特性
コンデンサに関する基本式:
\[ i_C = C \frac{dv_C}{dt} \]
ここで:
\(i_C\; [\mathrm{A}]\):コンデンサに流れる電流
\(C\; [\mathrm{F}]\):静電容量
\(\frac{dv_C}{dt}\; [\mathrm{V/s}]\):電圧の時間変化率
この式から、コンデンサは電圧の変化を妨げる性質を持つことがわかります。
時定数の概念
時定数(\(\tau\))は、過渡現象における重要なパラメータで、回路が初期状態から定常状態に至るまでの時間的な尺度を表します。
RL回路の時定数:\(\tau = \frac{L}{R}\; [\mathrm{s}]\)
RC回路の時定数:\(\tau = CR\; [\mathrm{s}]\)
時定数が大きいほど、過渡現象が収束するまでの時間が長くなります。
リアクトルの過渡現象
リアクトルの状態変化
①過渡状態(初期状態):リアクトルは電流値を維持しようとする働きをします。電圧を印加した瞬間はほとんど電流が流れないので、開放として考えます。
②定常状態(最終状態):電圧印加後、十分時間が経過すると、リアクトルの実効的な抵抗はほぼ零になります。したがって、短絡として考えます。
RL直列回路において、スイッチを閉じた瞬間からの電圧と電流の変化を見てみましょう。
図:RL直列回路
(直流電源 E、抵抗 R、リアクトル L が直列に接続された回路)
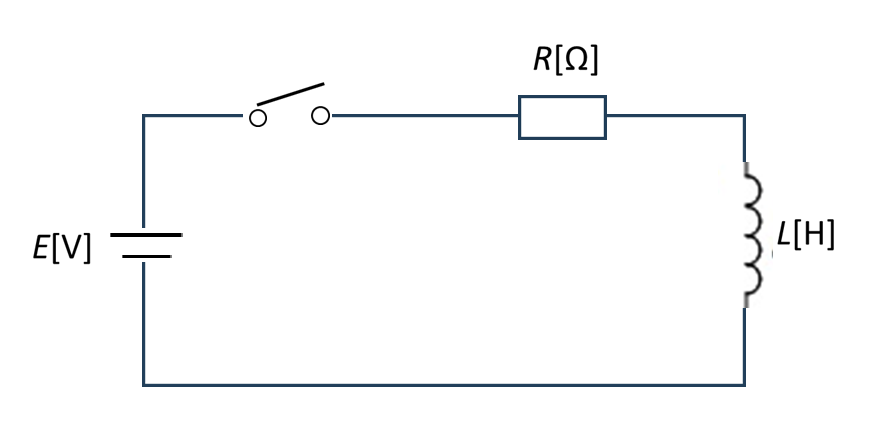
この回路において、スイッチを閉じた瞬間(t = 0)から電流は徐々に増加し、リアクトルの端子電圧は徐々に減少します。
リアクトル回路の過渡応答
RL回路における過渡応答は次の式で表されます:
\[ \begin{aligned} V_{\mathrm{L}} &= E \mathrm{e}^{-\frac{R}{L}t} \\[10pt] I_{\mathrm{L}} &= \frac{E}{R}\left(1-\mathrm{e}^{-\frac{R}{L}t}\right) \end{aligned} \]
ここで:
\(V_{\mathrm{L}}\; [\mathrm{V}]\):リアクトルの端子間電圧
\(I_{\mathrm{L}}\; [\mathrm{A}]\):回路を流れる電流
\(E\; [\mathrm{V}]\):電源電圧
\(R\; [\Omega]\):抵抗値
\(L\; [\mathrm{H}]\):インダクタンス
\(t\; [\mathrm{s}]\):スイッチを閉じてからの経過時間
時定数とリアクトル回路の関係
RL回路の時定数 \(\tau = \frac{L}{R}\; [\mathrm{s}]\) は、電流が最終値の約63.2%に到達するまでの時間を表します。
時間経過とリアクトル回路の状態:
t = 0:電流は0、リアクトルの電圧は最大(E)
t = τ:電流は最終値の約63.2%、電圧は初期値の約36.8%
t = 2τ:電流は最終値の約86.5%、電圧は初期値の約13.5%
t = 3τ:電流は最終値の約95.0%、電圧は初期値の約5.0%
t = 4τ:電流は最終値の約98.2%、電圧は初期値の約1.8%
t = 5τ:電流は最終値の約99.3%、電圧は初期値の約0.7%(ほぼ定常状態)
リアクトル回路の例題
電源電圧 E = 100 V、抵抗 R = 10 Ω、インダクタンス L = 50 mH のRL直列回路において、スイッチを閉じてから 5 ms 後のリアクトルの端子電圧と回路電流を求めよ。
\[ \begin{aligned} \text{時定数 } \tau &= \frac{L}{R} = \frac{50 \times 10^{-3}}{10} \\ \\[10pt] &= 5 \times 10^{-3}\,\mathrm{s} = 5\,\mathrm{ms} \\ \\[10pt] V_{\mathrm{L}} &= E\,\mathrm{e}^{-\frac{R}{L}t} \\ \\[10pt] &= 100\,\mathrm{e}^{-\frac{10}{50 \times 10^{-3}} \times 5 \times 10^{-3}} \\ \\[10pt] &= 100\,\mathrm{e}^{-1} \\ \\[10pt] &\approx 36.8\,\mathrm{V} \\ \\[10pt] I_{\mathrm{L}} &= \frac{E}{R} \left(1 - \mathrm{e}^{-\frac{R}{L}t} \right) \\ \\[10pt] &= \frac{100}{10} \left(1 - \mathrm{e}^{-1} \right) \\ \\[10pt] &= 10 \times 0.632 \\ \\[10pt] &\approx 6.32\,\mathrm{A} \end{aligned} \]
→ 横スクロールして下さい
この問題では、ちょうど時定数 τ と同じ 5 ms 経過した時点での値を求めているため、電圧は初期値の約36.8%、電流は最終値の約63.2%となります。
コンデンサの過渡現象
コンデンサの状態変化
①過渡状態(初期状態):コンデンサに蓄えられている電荷が零であるので、電流がものすごく流れやすい状態、すなわち短絡として考えます。
②定常状態(最終状態):コンデンサに十分に電荷が蓄えられているので、電流をこれ以上蓄えようとしない、すなわち開放として考えます。
RC直列回路において、スイッチを閉じた瞬間からの電圧と電流の変化を見てみましょう。
図:RC直列回路
(直流電源 E、抵抗 R、コンデンサ C が直列に接続された回路)
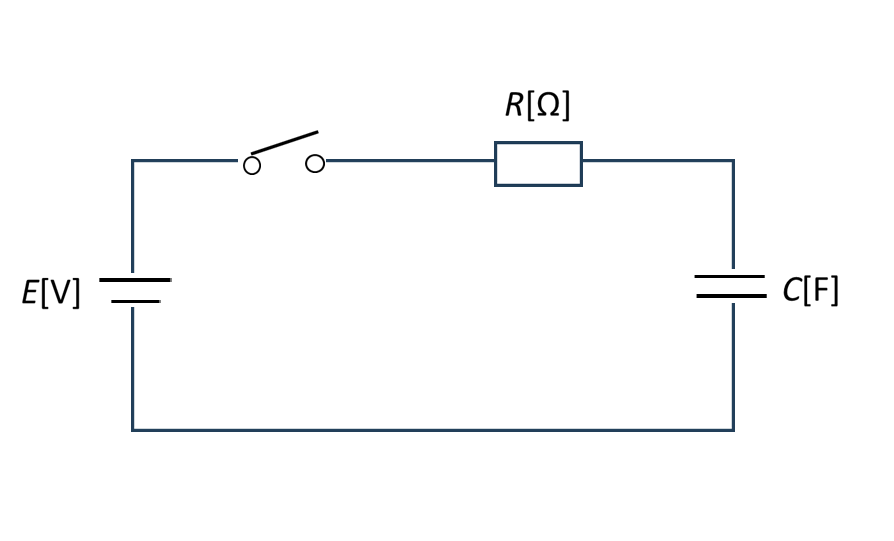
この回路において、スイッチを閉じた瞬間(t = 0)からコンデンサの端子電圧は徐々に増加し、電流は徐々に減少します。
コンデンサ回路の過渡応答
RC回路における過渡応答は次の式で表されます:
\[ \begin{aligned} V_{\mathrm{C}} &= E\left(1-\mathrm{e}^{-\frac{t}{CR}}\right) \\[10pt] I_{\mathrm{C}} &= \frac{E}{R}\mathrm{e}^{-\frac{t}{CR}} \end{aligned} \]
ここで:
\(V_{\mathrm{C}}\; [\mathrm{V}]\):コンデンサの端子間電圧
\(I_{\mathrm{C}}\; [\mathrm{A}]\):回路を流れる電流
\(E\; [\mathrm{V}]\):電源電圧
\(R\; [\Omega]\):抵抗値
\(C\; [\mathrm{F}]\):静電容量
\(t\; [\mathrm{s}]\):スイッチを閉じてからの経過時間
時定数とコンデンサ回路の関係
RC回路の時定数 \(\tau = CR\; [\mathrm{s}]\) は、コンデンサの電圧が最終値の約63.2%に到達するまでの時間を表します。
時間経過とコンデンサ回路の状態:
t = 0:電圧は0、電流は最大(E/R)
t = τ:電圧は最終値の約63.2%、電流は初期値の約36.8%
t = 2τ:電圧は最終値の約86.5%、電流は初期値の約13.5%
t = 3τ:電圧は最終値の約95.0%、電流は初期値の約5.0%
t = 4τ:電圧は最終値の約98.2%、電流は初期値の約1.8%
t = 5τ:電圧は最終値の約99.3%、電流は初期値の約0.7%(ほぼ定常状態)
コンデンサ回路の例題
電源電圧 E = 100 V、抵抗 R = 10 kΩ、静電容量 C = 10 μF のRC直列回路において、スイッチを閉じてから 100 ms 後のコンデンサの端子電圧と回路電流を求めよ。
\[ \begin{aligned} \text{時定数 } \tau &= CR = 10 \times 10^{-6} \times 10 \times 10^3 \\ \\[10pt] &= 0.1\,\mathrm{s} = 100\,\mathrm{ms} \\ \\[10pt] V_{\mathrm{C}} &= E\left(1 - \mathrm{e}^{-\frac{t}{CR}}\right) \\ \\[10pt] &= 100\left(1 - \mathrm{e}^{-\frac{100 \times 10^{-3}}{10 \times 10^{-6} \times 10 \times 10^3}}\right) \\ \\[10pt] &= 100\left(1 - \mathrm{e}^{-1}\right) \\ \\[10pt] &\approx 100 \times 0.632 \\ \\[10pt] &\approx 63.2\,\mathrm{V} \\ \\[10pt] I_{\mathrm{C}} &= \frac{E}{R} \mathrm{e}^{-\frac{t}{CR}} \\ \\[10pt] &= \frac{100}{10 \times 10^3} \mathrm{e}^{-1} \\ \\[10pt] &= 10 \times 10^{-3} \times 0.368 \\ \\[10pt] &\approx 3.68\,\mathrm{mA} \end{aligned} \]
→ 横スクロールして下さい
この問題では、ちょうど時定数 τ と同じ 100 ms 経過した時点での値を求めているため、電圧は最終値の約63.2%、電流は初期値の約36.8%となります。
計算例と応用
過渡現象の計算ステップ
1. 回路の時定数を求める(RL回路:\(\tau = \frac{L}{R}\)、RC回路:\(\tau = CR\))
2. 回路の初期状態と最終状態を把握する
3. 適切な過渡応答式を使用して、指定された時刻での値を計算する
4. 計算結果が理にかなっているか確認する(5τ経過後はほぼ定常状態になっているはずなど)
例題1:複合時定数のRL回路
抵抗 R = 20 Ω、インダクタンス L = 100 mH の直列回路に、初期電流 I₀ = 5 A が流れていた。この回路を短絡した場合、2 ms 後の電流値を求めよ。
\[ \begin{aligned} \text{時定数} \tau &= \frac{L}{R} = \frac{100 \times 10^{-3}}{20} = 5 \times 10^{-3} \; \mathrm{s} = 5 \; \mathrm{ms} \\[10pt] I &= I_0 \mathrm{e}^{-\frac{R}{L}t} = 5 \mathrm{e}^{-\frac{20}{100 \times 10^{-3}} \times 2 \times 10^{-3}} \\[10pt] &= 5 \mathrm{e}^{-0.4} \approx 5 \times 0.67 \approx 3.35 \; \mathrm{A} \end{aligned} \]
例題2:充電済みコンデンサの放電
静電容量 C = 47 μF のコンデンサに 24 V の電圧が充電されている。このコンデンサを抵抗 R = 10 kΩ で放電させた場合、コンデンサの電圧が 10 V になるまでの時間を求めよ。
\[ \begin{aligned} \text{時定数} \tau &= CR = 47 \times 10^{-6} \times 10 \times 10^3 = 0.47 \; \mathrm{s} \\[10pt] V &= V_0 \mathrm{e}^{-\frac{t}{CR}} \\[10pt] 10 &= 24 \mathrm{e}^{-\frac{t}{0.47}} \\[10pt] \frac{10}{24} &= \mathrm{e}^{-\frac{t}{0.47}} \\[10pt] \ln\left(\frac{10}{24}\right) &= -\frac{t}{0.47} \\[10pt] t &= -0.47 \times \ln\left(\frac{10}{24}\right) \\[10pt] &= -0.47 \times \ln(0.417) \\[10pt] &= -0.47 \times (-0.875) \\[10pt] &\approx 0.41 \; \mathrm{s} \end{aligned} \]
過渡現象の応用例
過渡現象の理解は、以下のような様々な電気回路の設計や分析に応用されます:
1. タイミング回路:リレー制御、タイマー回路など
2. スイッチング電源:電源立ち上げ時のサージ電流対策
3. モータ制御:始動時と停止時の過渡電流の制御
4. 電力系統保護:過渡現象による過電圧・過電流からの保護
5. 信号処理回路:RC回路を利用したフィルタリング
過渡現象の計算における注意点
1. 単位の統一:時定数の計算では単位を統一する(秒、ヘンリー、ファラド、オームなど)
2. 指数関数の計算:\(\mathrm{e}^{-1} \approx 0.368\)、\(1 - \mathrm{e}^{-1} \approx 0.632\) などの値を覚えておくと便利
3. 初期条件の確認:回路の初期状態(電流・電圧)を正確に把握する
4. 時定数の影響:時定数が大きいほど過渡現象の収束が遅くなることを理解する
電気主任技術者試験における過渡現象の出題ポイント
1. 時定数の計算と物理的意味の理解
2. 過渡現象の式を利用した特定時刻での電圧・電流の計算
3. コンデンサの充放電やリアクトルのエネルギー蓄積に関する計算
4. 電圧・電流が特定の値に達するまでの時間の計算
5. RL回路とRC回路の過渡特性の比較
🔍 ワンポイントアドバイス: 過渡現象を理解する際、リアクトルとコンデンサの初期状態と定常状態の性質(リアクトル:初期は開放→定常は短絡、コンデンサ:初期は短絡→定常は開放)を覚えておくことが重要です。また、時定数τの5倍(5τ)経過すると、回路はほぼ定常状態(最終値の約99%)に達することを覚えておきましょう。さらに、指数関数の計算では、t = τのときe^(-1)≒0.368、1-e^(-1)≒0.632という値を暗記しておくと、試験での計算が格段に速くなります。
理論 RC回路の過渡現象
ただし,自然対数の底は,\( 2.718 \)とする。
コンデンサを充電した後に放電する回路で、スイッチを切り替えた瞬間から何が起こるかを考えていくで。
一つずつ選択肢を検討していこか。
抵抗\( R \)とコンデンサの静電容量\( C \)の関係を教えてくれるかな?
つまり、\( \tau = RC \)です。
この式から、時定数はコンデンサの静電容量\( C \)に比例することがわかります。
したがって、(1)の記述は正しいと判断できます。
解説
正解は (5) です。
各選択肢の詳しい解説:
- (1) 正しい:RC回路の時定数\( \tau \)は、\( \tau = RC \)で与えられます。この式から明らかなように、時定数はコンデンサの静電容量\( C \)に比例します。
- (2) 正しい:コンデンサの放電時の端子電圧は\( v_{\mathrm{C}} = E \cdot e^{-\frac{t}{RC}} \)で表されます。抵抗\( R \)が大きいほど時定数\( RC \)も大きくなり、指数関数の減衰が緩やかになるため、電圧はより緩やかに減少します。
- (3) 正しい:時定数\( \tau = RC \)だけ時間が経過した場合、コンデンサの端子電圧は\( v_{\mathrm{C}} = E \cdot e^{-1} = E \cdot \frac{1}{2.718} \approx 0.368E \)となります。したがって、電圧は元の値の約36.8%に減少します。
- (4) 正しい:充電時にはコンデンサに向かって電流が流れますが、放電時にはコンデンサから電流が流れ出すため、電流の向きが逆転します。このため、抵抗の端子電圧の極性も充電時と放電時で逆になります。
- (5) 誤り:スイッチを2側に切り替えた直後(\(t=0\))の電流は、\( i(0) = \frac{v_{\mathrm{C}}(0)}{R} = \frac{E}{R} \)で与えられます。この式にはコンデンサの静電容量\( C \)が含まれていないため、初期電流の大きさは\( C \)の値に関係しません。ただし、時間経過後の電流の減少の仕方には\( C \)の値が関係します。
RC回路の過渡現象では、スイッチを切り替えた瞬間のコンデンサは電圧源として働き、その後時定数に従って指数関数的に放電していきます。時定数が大きいほど放電は緩やかになりますが、初期状態での電流は電圧と抵抗だけで決まるという点が重要です。
この問題のポイント
- RC回路の時定数: \(\tau = RC\)
- 放電時のコンデンサ電圧: \(v_{\mathrm{C}} = E \cdot e^{-\frac{t}{RC}}\)
- 放電時の電流: \(i = -\frac{E}{R} \cdot e^{-\frac{t}{RC}}\)
- 時定数経過後の値: 初期値の約36.8%(\(e^{-1}\)倍)
- \(t=0\)での電流は\(C\)に依存せず、\(E\)と\(R\)だけで決まる